はじめに:なぜ優秀なトレーダーも破産するのか
投資の世界には不思議な現象があります。勝率が55%もある、つまり負けるより勝つ方が多いトレーダーが、なぜか破産してしまうのです。一方で、同じ勝率でも着実に資産を増やし続ける投資家もいます。この違いは何でしょうか。
答えは「ポジションサイズ」にあります。どんなに優れた投資戦略を持っていても、一度に賭ける金額を間違えれば、最終的には資産を失ってしまいます。逆に、勝率がそこそこでも、適切な資金管理をすれば長期的に成功できるのです。
この記事では、1956年にベル研究所のジョン・L・ケリー・ジュニアが発見した「ケリー基準(Kelly Criterion)」について、Pythonシミュレーションを交えながら解説します。この数学的手法は、長期的に最も効率よく資産を増やすための賭け金を教えてくれます。
この記事で学べること
- ケリー基準の数学的な意味と公式
- なぜ過剰な賭けが破産を招くのか
- Pythonシミュレーションによる実証
- 実践的な投資への応用方法
ケリー基準の基本:シンプルな例から理解する
まず、非常にシンプルな賭けのゲームを考えてみましょう。コインを投げて、表が出たら賭け金が2倍になり、裏が出たら賭け金を全て失うとします。ただし、このコインは普通のコインではなく、55%の確率で表が出る、やや有利なコインです。
あなたの手元には100万円あります。このゲームを250回繰り返すとき、毎回いくら賭けるのが最適でしょうか。
直感的には「勝率が55%もあるなら、たくさん賭けた方が儲かる」と考えるかもしれません。しかし、これは大きな間違いです。実際にシミュレーションしてみると、驚くべき結果が見えてきます。
ケリー基準の公式
ケリー基準の公式は以下の通りです:
ここで、
- $f^*$:資産に対して賭けるべき割合
- $p$:勝率
- $q = 1 – p$:負率
- $b$:オッズ(この例では1、つまり勝てば2倍)
私たちの例(勝率55%、1:1のオッズ)に当てはめると:
f^* = \frac{1 \times 0.55 - 0.45}{1} = 0.10
つまり、毎回資産の10%を賭けるのが最適という結果になります。
重要なポイント
勝率55%でも、最適な賭け率はわずか10%です。直感よりもはるかに控えめな値になります。
Pythonシミュレーションで確かめる
理論だけでは実感が湧きにくいので、実際にシミュレーションしてみましょう。提供されたコードは、異なる賭け率で何千回もゲームを繰り返し、その結果を視覚化します。
ケリー係数の計算
kelly_fraction.py
def kelly_fraction(p: float, b: float = 1.0) -> float:
"""ケリー係数を計算する関数
Args:
p: 勝率
b: オッズ(勝った時の倍率 - 1)
Returns:
最適な賭け率
"""
q = 1.0 - p # 負率
return (b * p - q) / b
このシミュレーションでは、5000回の試行を行い、それぞれの賭け率がどのような結果をもたらすかを追跡します。重要なのは、平均値ではなく「期待対数成長率」という指標を使うことです。
なぜ対数成長率が重要なのか
投資の世界では、単純な平均利益ではなく「複利効果」が重要です。100万円が2倍になって200万円になり、それがまた2倍になれば400万円です。このような乗法的な成長を適切に扱うには、対数を使う必要があります。
期待対数成長率は以下の式で表されます:
g(f) = p \log(1 + bf) + (1-p) \log(1 - f)
この関数を最大化する $f$ が、ケリー係数 $f^*$ になります。シミュレーション結果の左側のグラフを見ると、まさにこの理論通りの曲線が描かれているのが分かります。
シミュレーション結果が教える3つの重要な教訓
第一の教訓:最適値を超えると成長率が急降下する
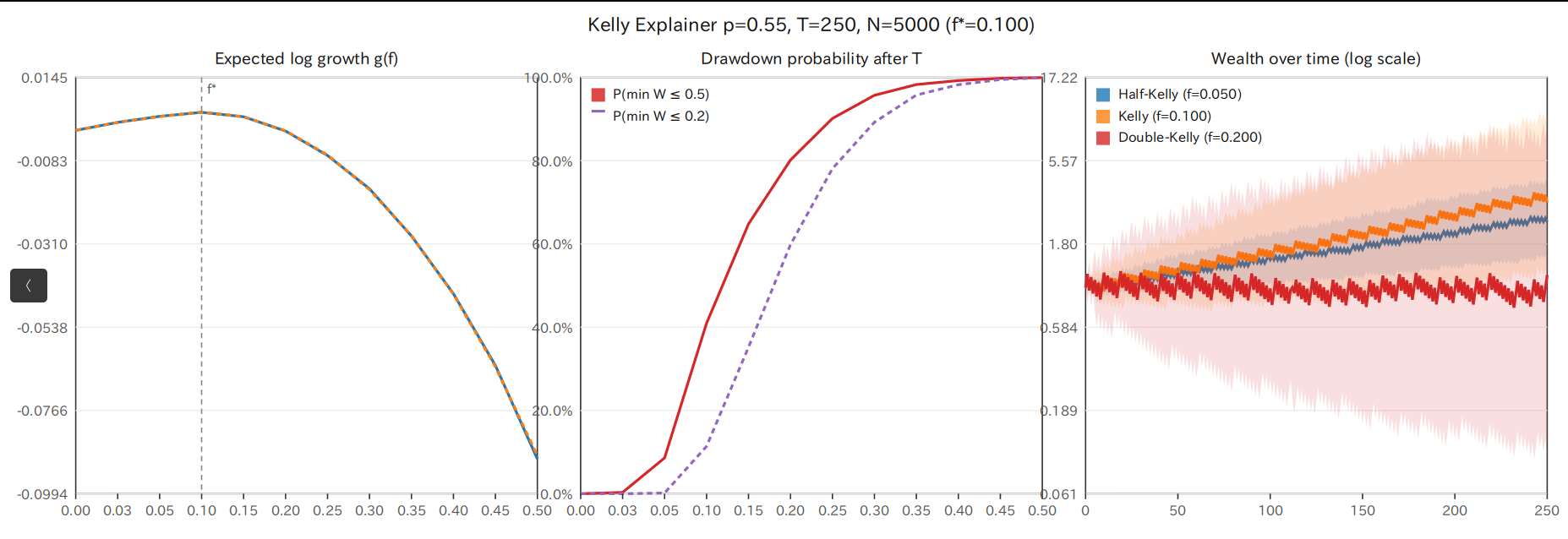
グラフの左側のパネルを注意深く見てください。青い実線が実際のシミュレーション結果、オレンジの点線が理論値です。両者はほぼ完全に一致しており、理論の正しさを示しています。
興味深いのは、ケリー係数(この場合0.10)のところで成長率が最大になり、それを超えると急激に下がることです。例えば、2倍の0.20を賭けると、成長率はマイナスになってしまいます。つまり、長期的には確実に資産が減っていくのです。
勝率55%でも20%賭けると損をする
「勝率が55%もあるのに、20%賭けたら損をする」というのは不思議に思えるでしょう。しかし、これが複利の恐ろしさです。一度大きく負けると、それを取り戻すのに何倍もの利益が必要になるのです。
第二の教訓:過剰な賭けは破滅的な損失をもたらす
中央のグラフは、さらに衝撃的な事実を示しています。これは「ドローダウン確率」、つまり資産が一定レベル以下に落ち込む確率を表しています。
赤い実線は「資産が元の50%以下になる確率」を示しています。ケリー係数の2倍(0.20)を賭けた場合、250回のゲームの間にほぼ100%の確率で資産が半分以下になります。紫の点線で示される「80%の損失」も、高い確率で発生します。
これは単なる理論上の話ではありません。実際の投資でも、レバレッジを効かせすぎたトレーダーが、一時的に大きな利益を上げた後、一度の暴落で全てを失う例は後を絶ちません。
第三の教訓:時間とともに差は指数関数的に開く
右側のグラフは、最も示唆に富む結果を示しています。これは時間の経過とともに資産がどう変化するかを、3つの戦略で比較したものです。
| 戦略 | 賭け率 | 特徴 |
|---|---|---|
| ハーフケリー | 0.05 | 非常に安定しているが、成長は緩やか |
| ケリー | 0.10 | バランスが取れており、着実に成長 |
| ダブルケリー | 0.20 | 激しく変動し、多くの場合で資産が減少 |
注目すべきは、色付きの帯域です。これは25パーセンタイルから75パーセンタイルまでの範囲、つまり中央50%のケースがどの範囲に収まるかを示しています。ダブルケリーの場合、この範囲が非常に広く、不安定であることが分かります。
時間が経つにつれて、適切な賭け率とそうでない賭け率の差は劇的に開いていきます。これが複利の力です。
実践への応用:理論を現実の投資に活かす
ここまでの説明で、ケリー基準の理論は理解できたと思います。しかし、実際の投資に応用するには、いくつかの重要な考慮事項があります。
勝率の推定という難問
ケリー基準の最大の弱点は、正確な勝率を知る必要があることです。シミュレーションでは勝率を55%と設定しましたが、実際の投資では勝率を正確に知ることはほぼ不可能です。
もし勝率を過大評価したらどうなるでしょうか。例えば、本当の勝率は50%(つまり優位性がない)なのに、55%だと思い込んで10%を賭け続けたとします。この場合、ケリー基準は $f^* = 0$ を示唆するはずですが、実際には10%を賭けてしまい、長期的には確実に損失を被ります。
ハーフケリー戦略の推奨
多くの実務家が「ハーフケリー」または「クォーターケリー」を推奨する理由は、理論上の最適値の半分、あるいは4分の1を賭けることで、推定誤差に対する保険をかけるためです。
複数の投資機会がある場合
実際の投資では、単一のゲームだけでなく、複数の投資機会が存在します。株式、債券、商品、為替など、それぞれに異なる勝率とオッズがあります。
この場合、各投資機会に対してケリー基準を適用し、それぞれの推奨ポジションサイズを計算します。ただし、単純に全てを合計すると、総ポジションが100%を大きく超える可能性があります。
この問題には、制約付き最適化という数学的手法で対処します。つまり、「全ポジションの合計が100%以下」という制約の下で、期待対数成長率を最大化するのです。これは、モダンポートフォリオ理論との興味深い接点でもあります。
心理的な側面:理論と実践のギャップ
どんなに優れた数学的手法も、実践できなければ意味がありません。ケリー基準の大きな課題は、推奨されるポジションサイズが、多くの人にとって心理的に受け入れがたいほど大きいことです。
例えば、勝率60%、オッズ2:1の非常に有利な投資機会があったとします。ケリー基準は33%、つまり資産の3分の1を賭けることを推奨します。しかし、資産の3分の1を単一の投資に投じることに、心理的な抵抗を感じる人は多いでしょう。
これは「リスク許容度」の問題です。数学的に最適であっても、夜眠れなくなるほどのリスクを取るべきではありません。ハーフケリーやクォーターケリーは、数学的効率を多少犠牲にしても、心理的な安定を得るための妥協点なのです。
コードの詳細:シミュレーションの仕組み
提供されたPythonコードは、非常に洗練された方法でケリー基準をシミュレートしています。いくつかの重要な部分を見てみましょう。
モンテカルロシミュレーション
run_simulation.py
def run_sim(
p: float = 0.55,
T: int = 250,
N: int = 5000,
b: float = 1.0,
fractions: List[float] = None,
seed: int = 42,
) -> Tuple[List[Dict], float]:
# 各賭け率について5000回の試行を実行
for f in fractions:
wealths: List[float] = []
log_growths: List[float] = []
for i in range(N):
# 各試行で250回のゲームを実行
w = 1.0 # 初期資産
lg = 0.0 # 対数成長率の累積
for _ in range(T):
if rng.random() p:
factor = 1.0 + b * f # 勝ち
else:
factor = 1.0 - f # 負け
w *= factor # 資産の更新
lg += math.log(factor) # 対数成長率の累積
このコードの巧妙な点は、破産の扱いです。賭け率が高すぎると、資産がゼロ、あるいはマイナスになる可能性があります。そのような場合、対数成長率を非常に大きな負の値(-1e9)に設定することで、破産のペナルティを適切に反映しています。
時系列データの生成
time_quantiles.py
def time_quantiles(
p: float,
T: int,
N: int,
b: float,
f_values: List[float],
seed: int,
qs: Tuple[float, float, float] = (0.25, 0.5, 0.75),
) -> Dict[float, Dict[str, List[float]]]:
# 各時点での25、50、75パーセンタイルを計算
この関数は、時間の経過とともに資産分布がどう変化するかを追跡します。これにより、右側のグラフの色付き帯域(インタークォータイルレンジ)を描画できます。中央値だけでなく、分布の広がりを見ることで、戦略のリスク特性をより深く理解できます。
SVG出力:依存関係のない可視化
このコードのもう一つの特徴は、matplotlibなどの外部ライブラリを使わず、SVGを直接生成していることです。これにより、依存関係を最小限に抑えつつ、美しいグラフを作成しています。
save_svg.py
def save_svg(path: str, results: List[Dict], meta: Dict) -> None:
# 座標変換の定義
def xmap(idx: int, panel: int) -> float:
t = 0.0 if len(fs) == 1 else idx / (len(fs) - 1)
return margin + panel * (panel_w + gutter) + t * panel_w
def y_g(v: float) -> float:
return margin + (1 - (v - g_min) / (g_max - g_min)) * panel_h
この部分は、データ空間からピクセル空間への変換を定義しています。数学的には線形変換であり、データの最小値と最大値を画面の上端と下端にマッピングします。
より深い理解のために:数学的背景
ケリー基準の背後にある数学は、情報理論と密接に関連しています。実際、ケリーの元論文は情報伝送の文脈で書かれました。
期待対数成長率を最大化することは、エントロピーを最大化することと等価です。より正確には、ケリー基準は、賭けによって得られる情報と、その情報を資産成長に変換する効率を最適化していると解釈できます。
中心極限定理との関係
十分に長い期間では、対数資産は正規分布に近づきます。これは中心極限定理の帰結です。ケリー基準は、この正規分布の平均を最大化する戦略と見なすことができます。
ただし、注意が必要なのは、これは「期待値」の最大化であり、「中央値」や「最頻値」の最大化ではないことです。右側のグラフを見ると、ダブルケリーの中央値はケリーよりも低いことが分かります。これは、ダブルケリーでは少数の幸運なケースが平均を引き上げているものの、典型的なケースではケリーに劣ることを意味します。
リスク調整後リターンの観点
現代の投資理論では、シャープレシオなどのリスク調整後リターンが重視されます。ケリー基準は、対数効用関数を仮定した場合の最適戦略と解釈できます。
対数効用関数は、リスク回避的な投資家を表しています。資産が2倍になる喜びは、資産が半分になる悲しみよりも小さいという感覚を数学的に表現したものです。この意味で、ケリー基準は単なる数学的最適化ではなく、人間の心理を反映した実用的な手法でもあります。
まとめ:ケリー基準から学ぶべきこと
この記事を通じて、ケリー基準が単なる賭け金の計算式ではなく、投資における根本的な原理を示していることが理解できたと思います。
最も重要な教訓
優位性があっても過剰な賭けは禁物
数学的に証明された最適値でさえ、実務では半分にすることが推奨されます。これは、不確実性と人間の限界を認識した、謙虚な姿勢の表れです。
次に、「時間が最大の武器」であることを忘れてはいけません。適切な資金管理のもとでは、わずかな優位性でも、時間をかければ劇的な差を生み出します。逆に、不適切な資金管理は、どんな優位性も無効化してしまいます。
最後に、理論と実践のバランスの重要性です。ケリー基準は美しい理論ですが、それを盲目的に適用するのではなく、自分のリスク許容度、推定の不確実性、市場の特性などを考慮して、適切に調整する必要があります。
投資成功の公式
投資で成功するための公式があるとすれば、それは以下のようなものでしょう:
\text{成功} = \text{優位性} \times \text{適切なポジションサイズ} \times \text{時間} \times \text{規律}
ケリー基準は、この公式の第二項を最適化する強力なツールです。しかし、他の要素、特に最後の「規律」も同様に重要です。どんなに優れた戦略も、それを一貫して実行できなければ意味がありません。
実際に試してみよう
シミュレーションコードを実際に動かして、パラメータを変えてみることをお勧めします。勝率を変えたり、オッズを変えたりすることで、ケリー基準の挙動をより深く理解できるでしょう。
実行コマンド
# シミュレーションの実行例
python simulate_kelly.py --p 0.55 --T 250 --N 5000
このコマンドを実行すると、kellyディレクトリに結果のCSVファイルと美しいSVGグラフが生成されます。これらを眺めながら、長期的な資産成長について考えてみてください。きっと、新たな洞察が得られるはずです。
参考文献
- Kelly, J. L. (1956). “A New Interpretation of Information Rate”. Bell System Technical Journal.
- Thorp, E. O. (2006). “The Kelly Criterion in Blackjack Sports Betting, and the Stock Market”.
- MacLean, L. C., Thorp, E. O., & Ziemba, W. T. (2011). “The Kelly Capital Growth Investment Criterion”.