様々なコンテキスト長における LLM の Self-Attention の Query と Key の分析

ABEJAでデータサイエンティストをしている藤原です。

今回は LLM のロングコンテキスト言語処理（Long-context language modeling; LCLM）に関連するブログになります。近年の LLM ではオープン・クローズド問わずより長大なコンテキストを正確に扱えるモデルが増えてきています。このようにロングコンテキストLLMが増えてくると、どのようにモデルのLCLM性能を評価すべきかが課題となります。

しかしながら、日本語の LCLM 評価のデータセットやベンチマークは現状なく、自作するにしても 128k トークンもある文章を人間が読んで品質を担保するのはかなり難しい問題だと思います。また、精緻な評価とはいかずとも、何かしらの方法で入出力・モデルの内部状態などを観察してモデルの LCLM 性能を分析できるとモデル開発・応用に役に立つと思っています。

そこで本記事ではLCLM ベンチマークなどで評価するのとは少し違った方法で、長文を入力した際のモデルの内部の状態を分析して、何かしら示唆が得られないか？という観点で検証してみました。具体的には Massive Values in Self-Attention Modules are the Key to Contextual Knowledge Understanding[1] という論文を参考に LLM の Self-Attention 層の出力を分析します。

1.1 はじめに

これまでの研究で残差ストリーム*1の活性に異常に大きな値（Massive Value）を示すこと、さらにこの Massive Value は Self-Attention における Query 層の出力（Q）と Key 層の出力（K）にのみ現れ、Value 層の出力（V）には見られないことが観測されています。

本研究ではこの現象について、 Massive Value がどのように形成されるのか、そしてそれがモデルの挙動とどのように結びついているのかを体系的に調査しています。主な発見は以下の4つです、

Q と K にだけ Massive Value が集中して現れる。特に、各ヘッドの特定の次元に集中して現れ、すべての Attention ヘッドでその位置が非常に似ている。この現象は V には見られず、 RoPE[3] を使わないモデルでも見られない。
Q と K の Massive Value は文脈的知識の理解に重要である。
3 . Massive Value を考慮した量子化手法は、文脈理解性能を保持する
Massive Value の集中はRoPEによって引き起こされる

1.2 Q, K における Massive Value の定義

現在主流の LLM における Attention の Q, K は、通常 $Q, K \in \mathbb{R}^{B \times S \times H \times D}$ で表されます。 $B$ はバッチサイズ（ここでは1を仮定）、 $S$ は系列長、 $H$ はヘッド数、 $D$ は各ヘッドの次元数です。massive value の判定では、Q, K について系列方向で L2 ノルムをとり、 $H \times D$ の行列 $M \in \mathbb{R}^{H \times D}$ に変換します。 Q について実際に式で書くと以下のようになります。

その上で、 Massive Value および集中した Massive Value について、論文中では次のように定義されています。

定義1. Massive Value
各ヘッドにおける次元 $d$ が、同ヘッド内の他次元の平均よりも $λ$ 倍以上大きい場合（経験的に $λ = 5$ を使用）：

定義2. Concentrated Massive Value
特定の次元に massive value が集中し、それが複数のヘッドで同じような位置に現れる現象。

例として論文中から Llama-2-7B の 10, 20 層目の Q, K の行列 $M$ を引用させていただきます。

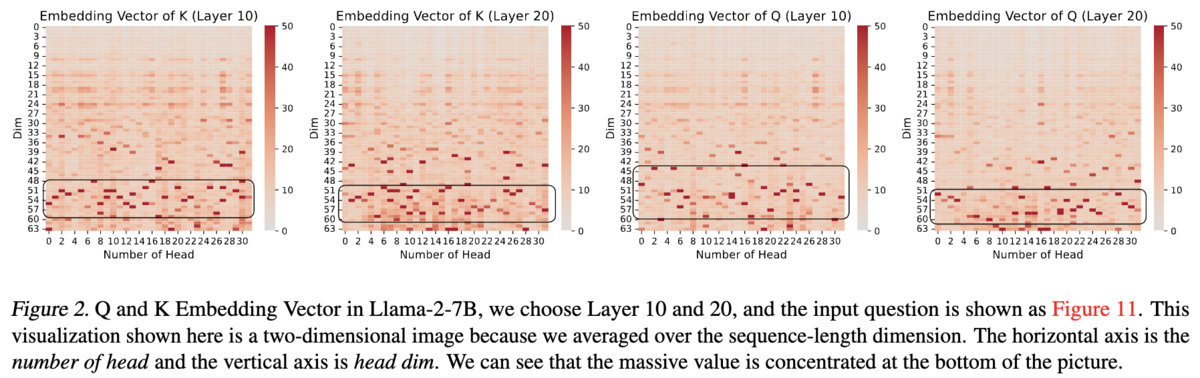
このグラフは横軸が Attention ヘッド数、縦軸が各ヘッドの次元数に対応していて、ヒートマップの値がヘッド $h$ 、次元 $d$ の行列 $M$ の値 $M_{h,d}$ に対応しています。

1.3 実験内容と結果

1.3.1. Massive Value は文脈知識理解に影響を与える

モデルが事前学習で獲得しているパラメトリックな知識と、入力コンテキストから獲得できる文脈的な知識のどちらに影響があるか調べる実験を行っています。パラメトリックな知識の理解・文脈的な知識の理解がそれぞれ重要となるタスクを用意し、 Prefill 段階の Q, K の Massive Value / 非Massive Value をそれぞれテンソル全体の平均に置換し、破壊の前後でスコアがどうなるか調べています。実験の結果、 Massive Value を破壊した場合はパラメトリックな知識が重要なタスクはスコアが低下するもののある程度は性能を維持しており、文脈的な知識の理解が重要なタスクでは著しく性能が低下しました。一方で、非Massive Value を破壊した場合はどちらもスコアの低下がない（文脈的な知識の理解が重要なタスクでは、むしろ少しスコアが上昇している）という結果でした。このことから、 Massive Value は文脈的な知識の理解において重要な要素であることが示唆されます。

1.3.2. Massive Value が集中する理由の分析

Massive Value がなぜ Q, K にのみ現れるか、一部の領域に集中して現れるのか、を明らかにするために、RoPE（Rotary Position Embedding）の仕組みに着目して分析しています。

1つ目に、 RoPE が使用されているモデルとそうでないモデルで比較すると、RoPE を使用するモデルでは一部の領域に Massive Value が集中する現象が見られるが、そうでないモデルはよりランダムに Massive Value が散らばっている、もしくは、Massive Value が現れないヒートマップになっています。そのため、（集中する） Massive Value は RoPE を採用するモデルに特有の現象の可能性があります。

2つ目に、 Massive Value が Q, K にのみ現れて V に現れないのは、 RoPE が適用されるのは Q, K のみであるからという可能性があります。これだけだと、RoPE による回転を適用することで Massive Value が現れており、学習されたモデル自体の性能には関係ない可能性があります。

そこで次のポイントに繋がりますが、 RoPE の回転の前後で Q, K を比較しても同様の Massive Value が観測されており、また入力に近い最初の層から Massive Value は観測されるため、 Massive Value は RoPE の適用自体によって発生するわけではなく、 RoPE を使用するモデルにおいて学習の結果として発生している可能性があります。

さらに、先ほど引用した Massive Value を可視化したヒートマップでもそうだったように Massive Value が Q, K の後半の次元（先ほどのヒートマップで下側の領域）に現れる傾向があります。これについては、後半の次元は RoPE の低周波領域であり、低周波領域は回転が小さく位置情報をあまり含まない領域になるため、意味的な情報を多く含むのではないか、という仮説を立てています。

ここからが本ブログでの検証になります。

紹介した先行研究 [1] では、 Massive Value が現れるのは RoPE を採用した学習済みモデルと考えられています。そこで気になったのは「RoPE を採用しているモデル同士の間での差異はあるのか？」という点です。そこで、同じベースモデルから異なる学習過程を経て構築されたモデル間では Q, K の行列 M や Massive Value の現れ方に違いがあるのか？」という観点で検証してみることにしました。特に以下の3つの観点で比較を行い、分析を行いました。

ロングコンテキスト対応のモデルを短いコンテキスト長で追加学習したらどうなるか？
- Qwen2.5 は最大 32k のコンテキスト長で構築されている。
- 一方で、それを継続事前学習して構築された ABEJA-Qwen では最大 8k という元のモデルよりも短いシーケンス長で追加学習されている（RoPE の設定などは元のモデルのまま）
ロングコンテキスト対応のモデルをより長いコンテキスト長で追加学習するとどうなるか？
- Qwen2.5-1M-7B は Qwen2.5-Instruct-7B をベースに追加学習を行い、 LCLM 性能を向上させている。
同じ規模のモデルで LCLM 性能に差があるモデル同士では違いがあるのか？
- Qwen2.5-Instruct と Qwen3 を比べると Qwen3 の方がロングコンテキストベンチマーク RULER において高いスコアを達成している。

さらに、冒頭でお話しした通り、 LCLM 性能との関係性があるのかも調べたいので、入力テキストは 2k, 4k, 8k, 16k, 32k, 64k, 128k トークンのテキストをそれぞれ 10個ずつ用意しました。使用したテキストは RULER ベンチマークの NIAH, QA タスクで合成できる質問文です。

分析方法は先行研究と同様で、（ヘッド数 × 次元数）サイズのヒートマップを図示し、それらを比較します。先行研究では RoPE の発生原因を探る目的から層ごとに描画して分析を行っていましたが、今回はモデル間の比較がメインのため全層での平均を描画して比較することにしました。分析するヒートマップの作成方法を整理すると以下のようになります。

それぞれのモデルにテキストを入力し、入力トークン長（2k, 4k, 8k, 16k, 32k, 64k, 128k）ごとに別々のヒートマップを作成
各入力トークン長についてそれぞれ 10 個のテキストを用意したため、10サンプルの平均を描画
行列 $M$ の算出方法は同じだが、層方向に平均をとったものを描画

先行研究[1] では短めのテキスト一つのみを使って分析しており、複数のテキストでの平均を取るような分析は行なっていません。比較するモデルの一覧は以下の通りです。

4.1 ロングコンテキスト対応のモデルを短いコンテキスト長で追加学習したらどうなるか？

Qwen2.5-7B-Instruct とそれを日本語で追加学習した ABEJA-Qwen2.5-7b-Japanese-v0.1 を比較しました。 ABEJA-Qwen はロングコンテキストを意識した追加学習は行っていないことと、シーケンス長 8k で追加学習しているため、元のモデルよりも LCLM 性能は低下している可能性があります。

それぞれのモデルの入力トークン長別の Q, K のヒートマップが以下です。各ヒートマップの縦軸は埋め込み次元のインデックスで、一番上が 0 次元目（RoPEの高周波領域）、一番下が 128 次元目（RoPEの低周波領域）になっています。横軸は Attention ヘッドのインデックスで Qwen2.5-7B-Instruct におけるヘッド数は Q が 28 、 K が 4 となっています。*2また各画像内で横に並んでいる複数のヒートマップは、左から入力トークン長が 1k, 2k, 4k, 8k, 16k, 32k, 64k, 128k の時の結果です。

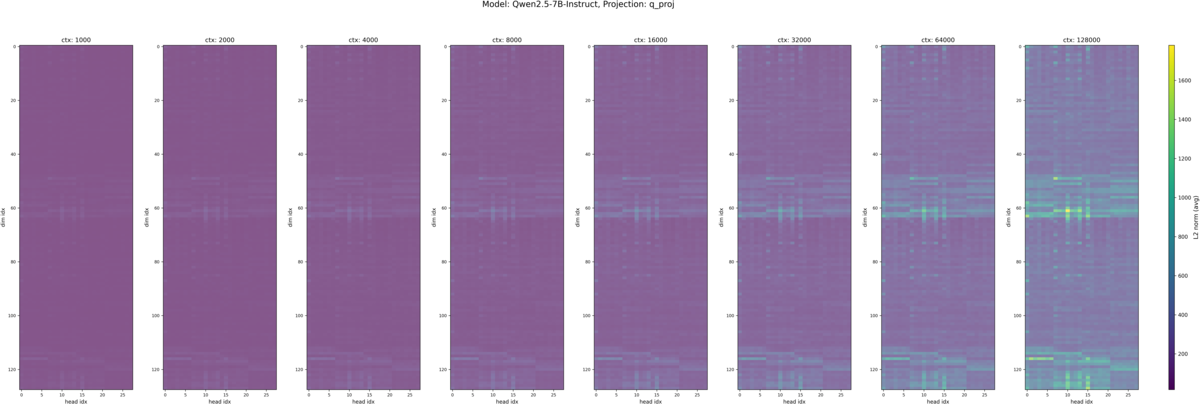
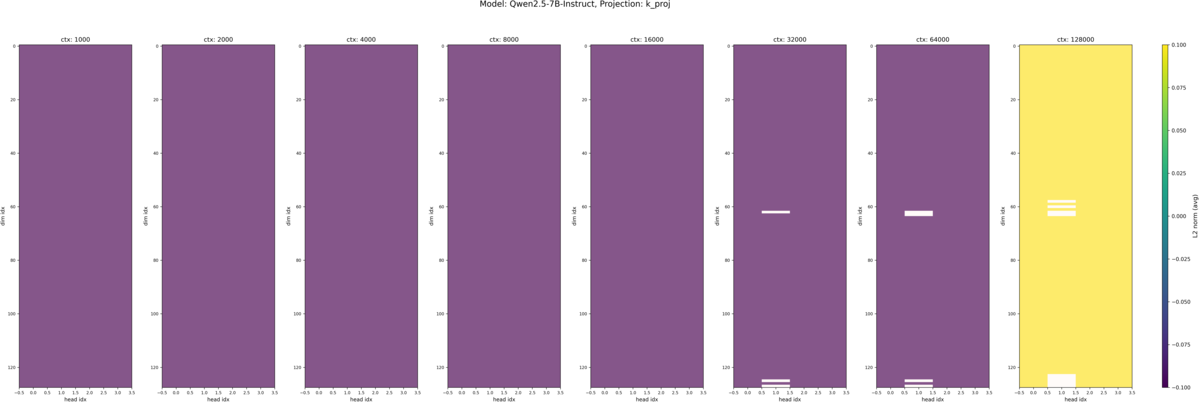
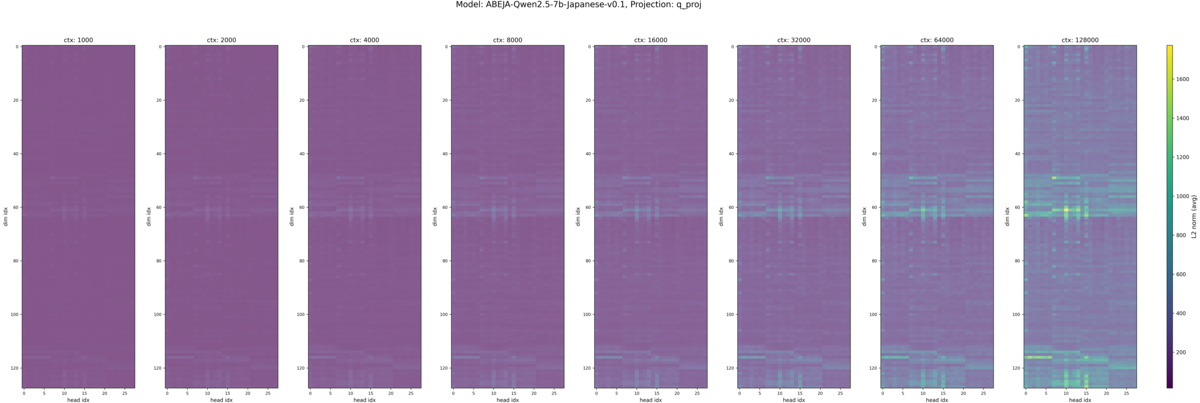
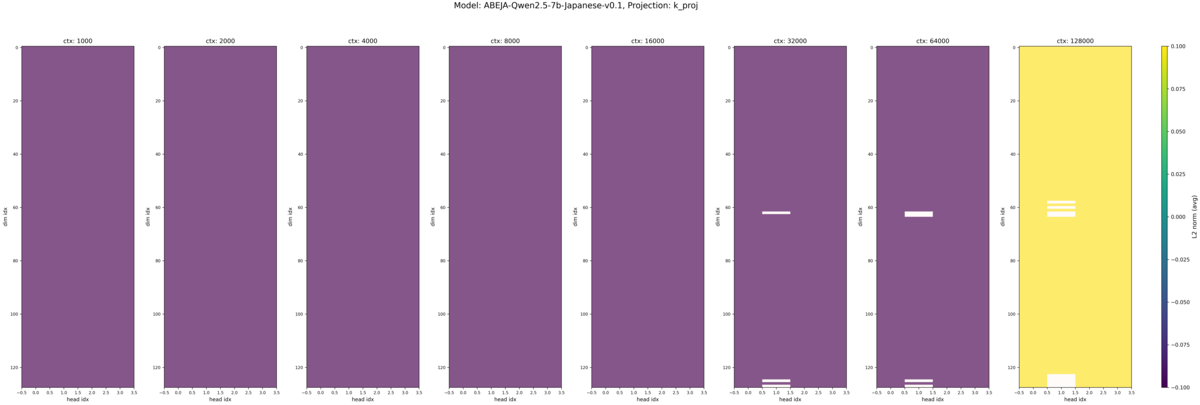
この図から

Q 固有
- 基本的に値のスケールが大きい
K 固有
- 基本的に値のスケールが小さい
- 32k （デフォルトで扱えるコンテキスト長のギリギリ）以上では、一部、スケールの範囲を超えた値が白く表示されている。（スケールは最大値・最小値で自動調整される設定にしていたため、適切な表示になっていない可能性がある）
Q, K 共通
- 入力長が長くなると、Query, Key の値が平均的に大きくなる
- Massive Value の現れる次元はヘッド間で共通している（先行研究と同じ結果）
- Massive Value の現れる次元は入力トークン長が増減しても同じ
- Massive Value は低周波だけでなく、中間の周波数帯にも現れている

ということが見て取れるかと思います。モデル間の違いについてはほとんど見受けられません。 K のグラフでは各図のカラーバーの上下限（色スケール）を 1k〜128k で共通化している影響で値の大小関係が正確にはわかりませんが、白く値が飛んでいる領域は Q で Massive Value が現れている周波数帯と同じになっています。 Massive Value が現れる周波数帯については、先行研究と少し異なり中間の周波数帯でも Massive Value が現れており、先行研究で述べられている「RoPE を採用しているモデルでは Massive Value が低周波数領域に集中する」という仮説と少し異なる結果になりました。

補足として、レイヤー別の結果も簡単に確認したところ、先頭・最終層付近の層の Q, K では同様の位置に Massive Value がみられ、中間付近の層では他の層ほど集中的な Massive Value は見られませんでした。層ごとの違いについては今回の分析対象ではなかったため、詳しい分析はしていませんが、層ごとの役割・得意不得意の違いと関係性があるのかもしれません。

4.2. ロングコンテキスト対応のモデルをより長いコンテキスト長で追加学習するとどうなるか？

Qwen2.5-7B-Instruct とそれをベースにコンテキストを拡大した Qwen2.5-7B-Instruct-1M を比較しました。LCLM 性能の参考として RULER ベンチマークでのスコアを記載します[4]。

モデル	4k	8k	16k	32k	64k	128k
Qwen2.5-7B-Instruct	96.7	95.1	93.7	89.4	82.3	55.1
Qwen2.5-7B-Instruct-1M	96.8	95.3	93.0	91.1	90.4	84.4

Qwen2.5-7B-Instruct （再掲）, Qwen2.5-7B-Instruct-1M の入力トークン長別の Q, K のヒートマップが以下です。

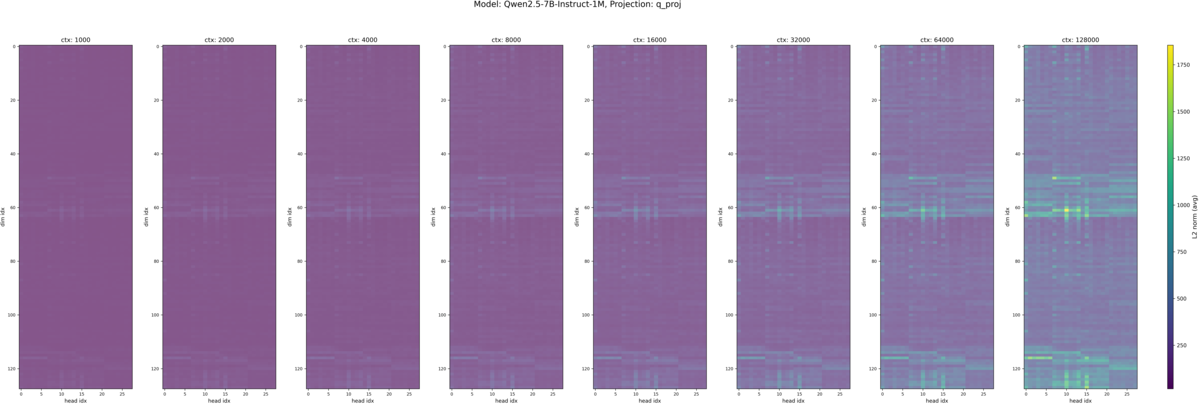
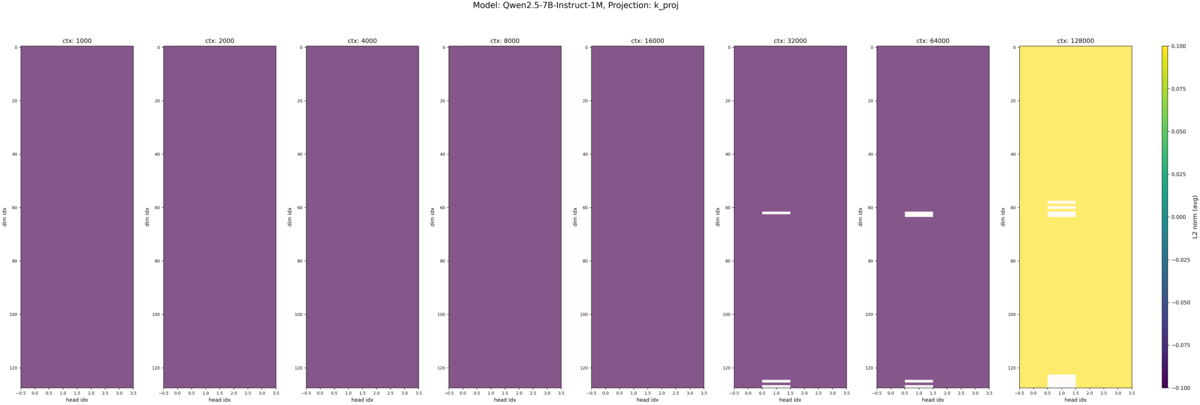
先ほどの Qwen2.5-7B-Instruct と比較して大きな違いは見られませんでした。強いて言えば、 Qwen2.5-7B-Instruct-1M – K の方が最大値が少し大きい程度でしょうか。LCLM 性能と関係性がありそうなモデル間の違いは見つけられませんでした。

4.3. 同じ規模のモデルで LCLM 性能に差があるモデル同士では違いがあるのか？

Qwen2.5-7B-Instruct と同規模でより高性能なモデルである Qwen3-8B を比較しました。 RULER ベンチマークでのスコアは以下です[5]。

モデル	4k	8k	16k	32k	64k	128k
Qwen2.5-7B-Instruct	96.7	95.1	93.7	89.4	82.3	55.1
Qwen3-8B (non-thinking)	96.3	96.0	91.8	91.2	82.1	77.4
Qwen3-8B (thinking)	94.7	94.4	86.1	80.8	78.3	72.0

Qwen2.5-7B-Instruct （再掲）, Qwen3-8B の入力トークン長別の Q, K のヒートマップが以下です。

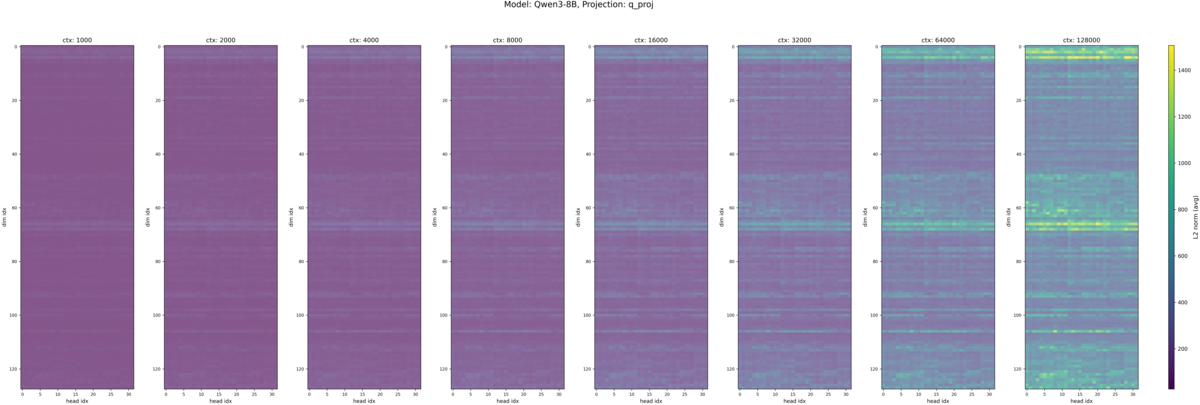
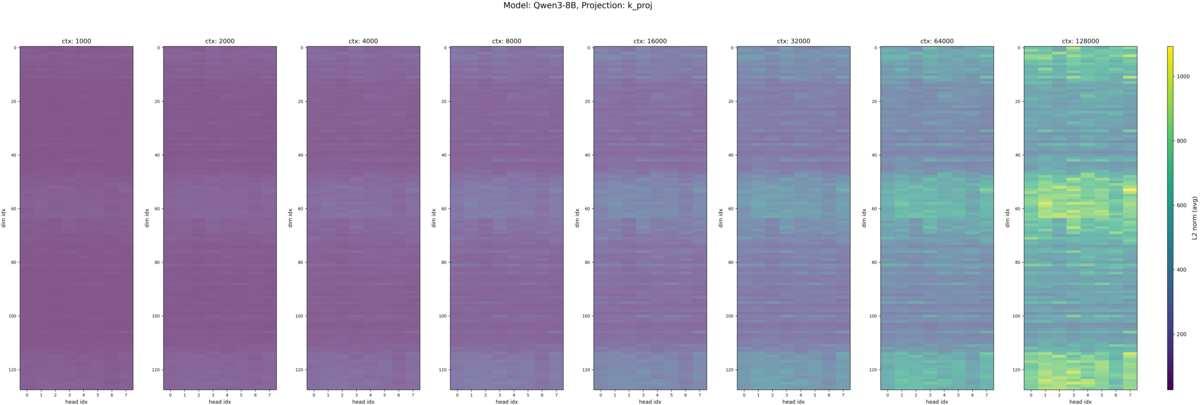
Q の値のスケールは Qwen2.5-7B-Instruct と同程度になりました。一方で、 K の値は Qwen3-8B では Q に近い値のスケールとなりました。また、 Massive Value が集中する領域については

Qwen2.5-7B-Instruct と同じ点
- ヘッド間で位置が一貫しているのは Qwen2.5-7B-Instruct から変わらず（先行研究と一致）
- Massive Value が集中する周波数帯は入力トークン長が増減しても同じ
Qwen2.5-7B-Instruct と異なる点
- Massive Value が集中する周波数帯は Qwen2.5-7B-Instruct では中間・低周波の領域であったが、 Qwen3 では高周波領域にも Massive Value が現れている

という結果になりました。この分析だけでは集中する領域の違いが LCLM 性能とどのような関係があるか判断できませんが、

Qwen3 では Qwen2.5 よりもロングコンテキストを意識した学習が行われており、特に 32k トークンのテキストを大量に学習している。
先行研究 [1] から
- 学習過程を経て低周波領域に Massive Value が集中するようになった可能性（仮説）
- Massive Value は文脈的な知識の保持に関係性がある（実験結果として示されたこと）

というのを踏まえると、長文のデータをより多く学習するほど、低周波領域での位置情報の重要性が高まり、他の周波数帯でも意味情報の比重を上げて、ロングコンテキストにおいても意味情報をうまく保持できるように学習されたのかもしれません。（単純にモデルの構成の違いが影響している可能性も十分にあります。）

各検証結果についてまとめると、

ロングコンテキスト対応のモデルを短いコンテキスト長で追加学習したらどうなるか？
- モデル間の違いはほとんど見られない
- ヘッド間で Massive Value の位置が一貫している（先行研究と一致）
- 入力コンテキスト長を変えても、値が大きくなる領域はあまり変わらない（先行研究と異なり低周波領域に集中するとは限らない可能性）
ロングコンテキスト対応のモデルをより長いコンテキスト長で追加学習するとどうなるか？
同じ規模のモデルで LCLM 性能に差があるモデル同士では違いがあるのか？
- モデル間で差がない部分
  - ヘッド間で Massive Value の位置が一貫している（先行研究と一致）
  - Massive Value が集中する周波数帯は入力トークン長が増減しても同じ（検証1, 2と同様）
- モデル間で差がある部分
  - Massive Value が集中する周波数帯は Qwen2.5-7B-Instruct では中間・低周波の領域であったが、 Qwen3 では高周波領域にも Massive Value が現れている