今年このブログでは、何度かTransformerなど自己回帰モデルベースのLLM/生成AIには「帰納的推論は出来ても演繹的推論が出来ていないが故の問題がある」という議論を扱ってきました。
例えば7月の記事では「世間で広く知られている複雑な論理パズルと、それと同じパズルの一部を改変した『自明』なパズルとのペアを多数用意して、主要なLLM/生成AIのCoT推論エンジンに回答させたところ、自明なパズルの正答率が一貫して元のパズルの正答率よりも低かった」という論文を紹介しました。この論文では「事前学習データに含まれているであろう論理パズルならどれほど複雑でも解けるのに、そのパズルを改変したらどれほど簡単でも解けなくなる」ことから、「LLM/生成AIのCoT推論は基本的には(事前学習データに対する)パターンマッチングに過ぎず、真の論理的推論とはいえない」と主張しています。
また8月の記事では「厳密に条件統制されたデータセットを用意してそれのみでLLMとそのCoT推論エンジンを事前学習させた上で、事前学習データ(とその推論プロセス)から僅かに改変された推論課題を多数用意して解かせたところ、事前学習データからの逸脱度に応じて正答率が低くなった」という論文を紹介しています。この論文では「CoTの推論能力は真の論理的推論のメカニズムではなく、洗練され構造化されたパターンマッチングの一形態であり、根本的に訓練時に見たデータ分布によって制限される」と指摘しています。
そしてこれらの論文で指摘される前から、Transformerというか「統計的学習」というパラダイムに依存するLLM/生成AIは原理的に「過去のデータや事例から一般的な法則を見出そうとする」帰納的推論に頼りがちで、それと本来対になるべき「所与のルールや法則を実際のデータや事例に当てはめる」演繹的推論が苦手(あるいは出来ない)という議論は長く続けられてきています。つい最近もLLMの算術計算はヒトが演算規則に従って行うそれとは仕組みが大幅に異なるらしいと指摘する研究が出ており(LLMのキモい算術 – ジョイジョイジョイ)、この課題点が根強いことが示された格好です。
そこで、僕個人としてはダイレクトに「LLM/生成AIに帰納的推論だけでなく演繹的推論をする能力を与えようという取り組みはないものか」と考えて、色々と調べてみたのでした。それがこちらの2024年に公開された論文(ACL2025に採択)です。
“The Role of Deductive and Inductive Reasoning in Large Language Models”とタイトルは大雑把ですが、LLMに帰納的推論だけでなく積極的に演繹的推論をさせようとしたというものです。その内容が結構面白かったので、今回の記事ではこちらの論文を紹介してみようと思います。
問題提起:帰納的推論しか出来ないLLMは演繹的推論さえ出来れば容易な課題を間違えてしまう
本論文のIntroductionにおける問題提起は明快で、LLMが上掲論文でも指摘されているような*1「どれほど複雑な課題でも事前学習されていれば解けるが、どれほど簡単な課題であっても事前学習次第では解けないことがある」点への改善を提案しようというものです。
特に、本論文では現在のLLMの限界点について「訓練中に学習した静的なプロンプト構造とパターンに依存していること」と指摘し、「これが新しい状況や進化する状況への適応性を制限している」とはっきりと述べています。そして重要な点として、そういった柔軟性の無さが反復的かつ適応的な典型的なヒトの問題解決アプローチとは対照的だと指摘しています。即ち「ヒトは帰納的推論を用いて特定の事例から一般的な規則を導き出し、その後、演繹的推論を新たな状況に適用することで、課題の複雑さに応じて動的な戦略調整を可能にしている」。これに対して「LLMは推論においてこのレベルの柔軟性を欠いており、より高度なシナリオへの一般化と適応能力が制限されている」という。
これらの問題点に対しては既に様々なアプローチによって解決が試みられてきていますが、大幅な基盤モデルの改修や計算リソースの追加が必要になるものが多かったと指摘されています。そこで、本論文ではプロンプト構築フレームワーク内に帰納的推論プロセスと演繹的推論プロセスの二者を統合する、つまりプロンプト自体を事前に定められたアルゴリズムに従って帰納と演繹とに多段階に分割して入力させる、というアプローチを提案しています。これなら基盤モデル自体には手を入れる必要がなく、計算リソースも固定したままで使える、というわけです。
アプローチ:適切な論理パズルを用意した上で「帰納→演繹→帰納→演繹……」と誘導する推論プロセス、DID (Deductive and InDuctive method)を多段階のプロンプトで与える
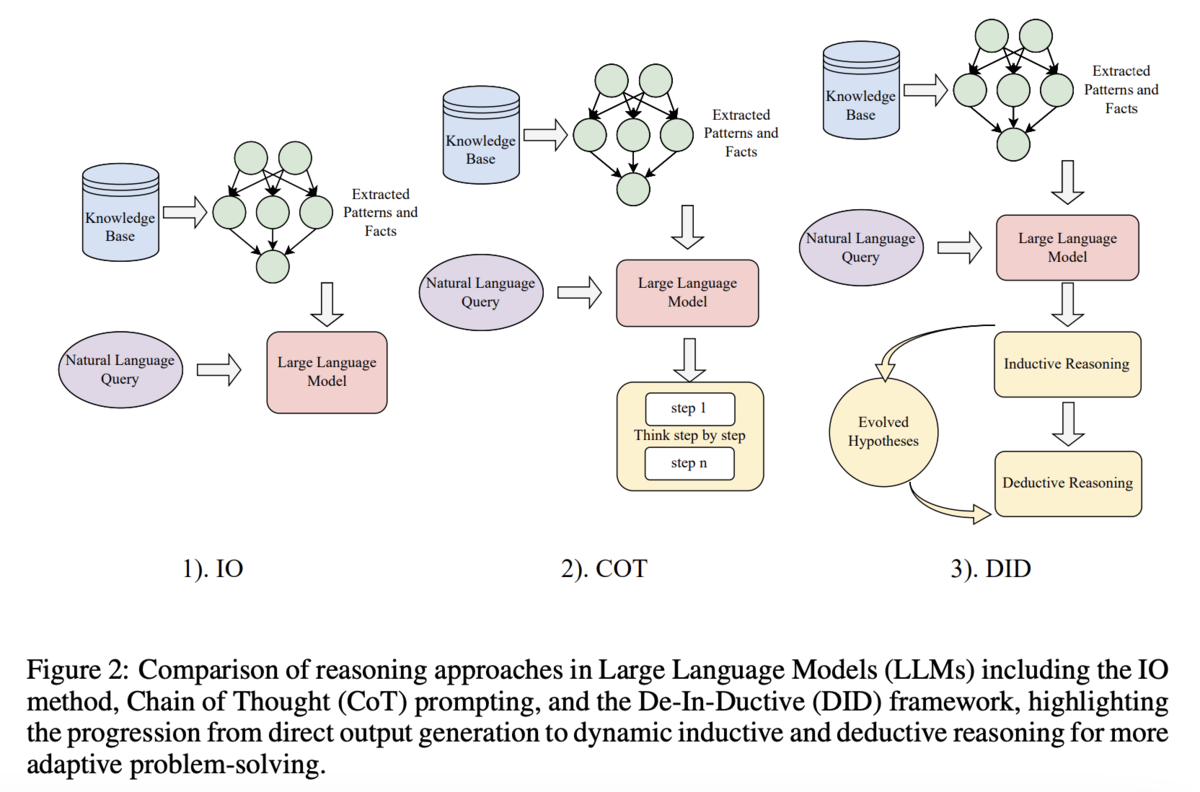
本論文のアプローチは、改めてFigure 2にまとめられています。要は「帰納→演繹→帰納→演繹……」と誘導する推論プロセスを多段階のプロンプトに分割してLLMに与えるというもので、DID (Deductive and InDuctive method)と呼称されています*2。

詳細なアルゴリズムはこちら。細かい説明がMethodsセクションにありますが、要約すると「その問題が持つ本質的な複雑さ」*3と「問題の条件として与えられる数値などの特徴に由来する複雑さ」「問題の規模」といった要素をもとに問題の複雑さを評価し、その上で問題を「帰納」「演繹」の各パートに確実に解決可能なレベルにまで細かく分解していき、最終的に問題全体を解決できるようにする、というものです。
性能評価に用いられたのは、Alice Problem, MR-GSM8K, Holiday Puzzleの3課題カテゴリ。Alice Problemは先行研究*4で示されたLLMにとっての困難課題の一つで「アリスにはN人の兄弟がいて彼女にはM人の姉妹がいる、アリスの兄弟から見て姉妹は何人いるか?」というヒトからは極めて容易に見えるのにLLMが間違えやすい課題です。MR-GSM8Kは広く用いられているメタ推論ベンチマークです*5。Holiday Puzzleは本論文で考案されたもので、過去10年間の中国における祝日の制定パターンに基づくそうです。ちなみに中国では特別祝日(国慶節・春節・労働節・中秋節など)に際して連休を作るために政府が複雑なカレンダー調整を毎年かけるとのことで、演繹的推論能力を測る上ではうってつけのベンチマークのように見えます。
実験対象のLLMは2024年当時利用可能だった主要なものということで、GPT-3.5 Turbo, GPT-4o, Claude 3.5 Sonnetが選ばれています。性能比較の都合のため、全ての推論パラメータはデフォルトで揃えたとのことです。
実験結果:DIDは演繹的推論を必要とする論理パズルの解答率を向上させた
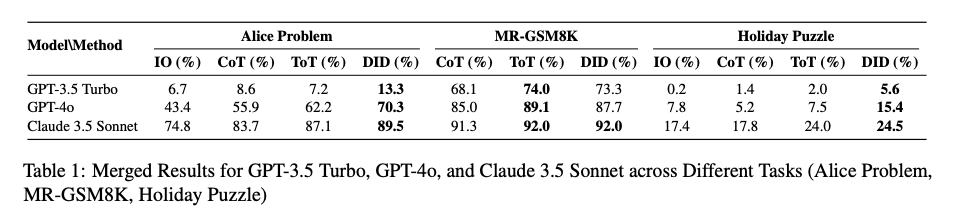
主要な実験結果がTable 1にまとまっています。見れば一目瞭然で、Alice ProblemとHoliday PuzzleではDIDが3つ全てのLLMでトップスコアを叩き出しています。MR-GSM8Kだけは広く普及しているベンチマークなせいか既存手法がトップスコアを出していますが、Claude 3.5 SonnetだけはDIDも同率トップスコアを出しています。
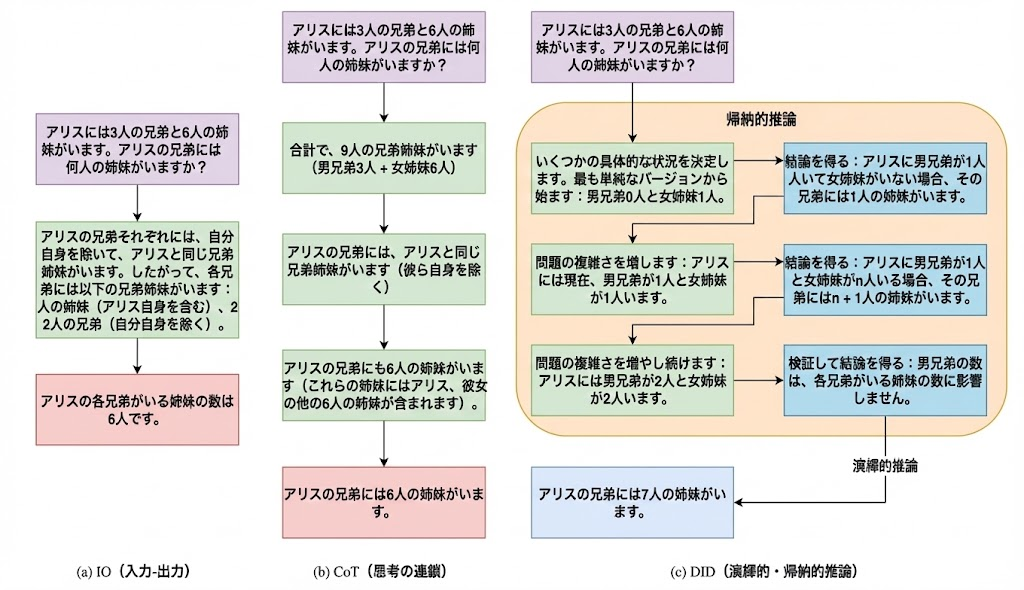
Figure 3にAlice Problemにおける既存手法とDIDの推論プロセスの詳細がまとめられていて(Appendix Bに詳細がある)、比べてみると面白いです。DIDでは一度数学的帰納法という演繹的推論*6にかけてから、正答に至っていることが分かります。
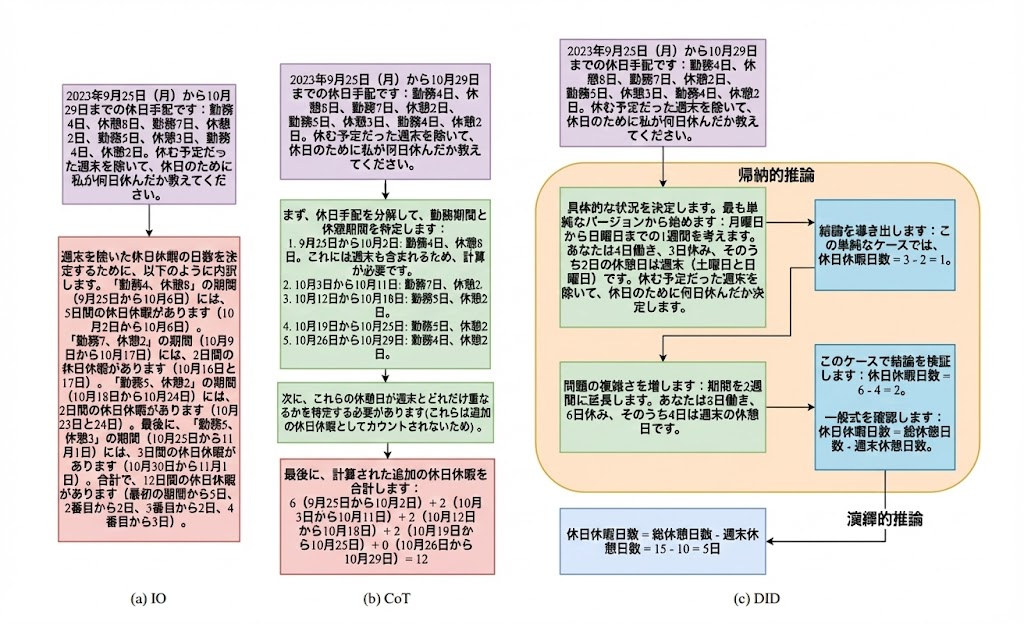
同様にFigure 4にはHoliday Puzzleにおける既存手法とDIDの推論プロセスの詳細がまとめられています。DIDではAlgorithm 1で提示された通りの推論プロセスを忠実に実行していることが見て取れます。
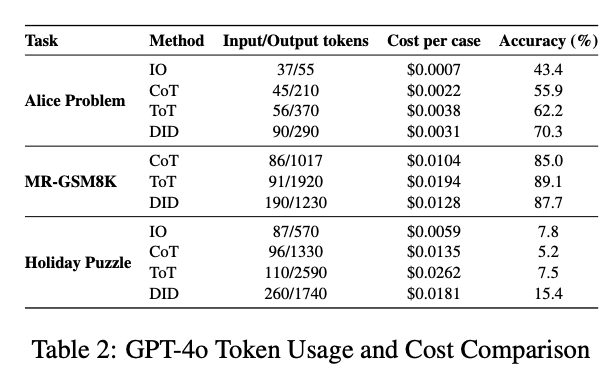
なおTable 2にはGPT-4oの各実験におけるトークン数とコストがまとめられています。全体として、DIDは比較的少リソース・低コストで回せているということが言えそうです。
ということで、DIDフレームワークによる帰納的&演繹的推論の統合が課題推論プロセスの改善に有効であるというのが本論文の結論ですが、それでも将来の課題として「そもそもLLM自体が複数の推論ステップに渡って一貫した内部表現を維持できていないのでロバスト性に問題がある」「別のベンチマークでも試してみなければ何とも言えない」と、慎重なコメントも残しています。
コメントなど
個人的にはかなり面白い論文だと思ったんですが、日本語圏でこれまでにこの論文を紹介した記事や資料がほぼ見当たらないところを見ると、あまり注目を集めなかったようです。それが「単に結果が面白くない・それほど劇的でもない」と受け取られたせいなのか、それとも「そもそもLLMに演繹的推論が必要だと考える人が少ない」せいなのかは分かりませんが、ちょっと意外だなと思いました。機械学習業界・LLM業界の方で、その辺の事情が分かる方いらっしゃいましたら、是非コメントなどでご教示いただけると幸いです。
特に、DIDアルゴリズム&プロンプトが初見の推論課題に対して必ず適切に構築できるかというとちょっと疑問に感じていて、その意味でももっと広汎な推論課題ベンチマークに対してどれくらいのパフォーマンスを出せるかを知りたいところです。
ただ、本論文を読んでちょっと思ったのが「ではヒトの演繹的推論って本当にこんなに複雑なんだろうか?」ということ。例えばAlice Problemでは、大半の人が「アリスは女性なのだからMにアリスを加えてM+1名とすれば良い」とすぐにロジカルに考えるのではないかと推察しますが、Figure 3を見ての通りDIDでは一度数学的帰納法を通しています。結局のところ事前学習データ(エピソード記憶)とは別に普遍的規則を覚えているからこそのヒトの推論プロセスだということなのだろうと、思う次第です。
ではそれを実現できるアーキテクチャはないのか?ということで実はこの記事を書く前にYann LeCunのWorld models*7についても調べたのですが、まだ議論が熟していないという印象だったので今回は選びませんでした。もう少し各方面での議論が深まってきたら、取り上げてみようかと思います。
余談
この記事中で紹介したFigure 3 (Alice Problem)とFigure 4 (Holiday Puzzle)ですが、オリジナルの図をNano Banana Proに読み込ませて、英語テキスト部分を日本語に翻訳させた上で体裁そのままに描き直させたものです。何だかんだ言って、生成AIのおかげで便利な世の中になったなぁと思いますね(笑)。

