本記事では、現在進行中で取り組んでいるテーマ「生成AI×数理最適化」に関する試みとして、生成AIを活用して数理最適化技術の実務適用を支援するアプローチを紹介します。例として、スーパーマーケットにおける在庫管理の効率化を取り上げ、その具体的な応用と効果について述べます。
はじめに
こんにちは、イノベーションセンター テクノロジー部門 先端AI数理PJの伊藤です。
普段はNode-AIやAI Autopilot Systemなどのプロダクト価値向上に加え、お客さまから寄せられる課題に対してデータ分析を通じた解決策の研究開発に取り組んでいます(例えば学習速度と変数選択精度を極めたFastGSCADモデル (Ver. 3.22.0)|Node-AI by NTTドコモビジネスなど)。
昨年度は機械学習×数理最適化で業務プロセス革命! – NTT docomo Business Engineers’ Blogという記事を執筆し、ありがたいことに多くの反響をいただきました。現在も、予測結果を活用した数理最適化技術の研究開発を継続しており、最近では、数理最適化による課題解決を支援する生成AIの活用の研究にも注力しています。
本記事では、スーパーマーケットにおける在庫管理を一例に、生成AIによる支援を活用した数理最適化技術による課題解決のアプローチをご紹介します。
背景
数理最適化モデルの定式化と実装に伴う困難
数理最適化では、現実に存在する課題を以下の形式に抽象化し、数学的モデルとして表現することが求められる場面は多くあります。
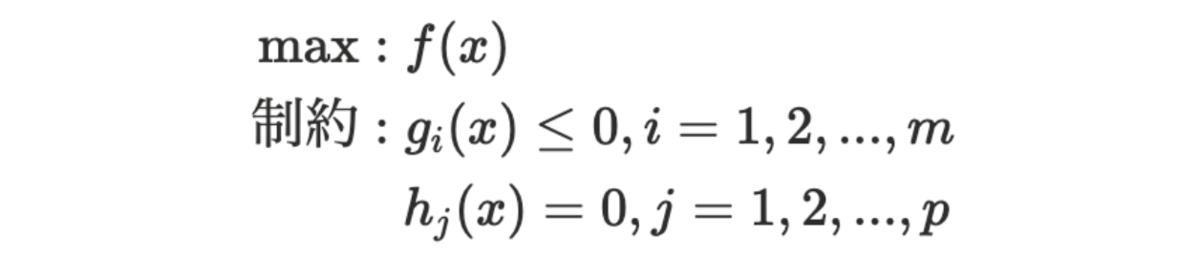
具体的には、個の不等式制約と
個の等式制約を満たしながら、問題の解を決めるための変数
を調整し、目的関数
を最大化する解を求めることを指します。
例えば、こちらの記事で取り上げているコールセンターにおけるオペレーター最適配置の課題では、課題の整理から出発し、以下のような数理最適化モデルへと定式化を行っています(詳しくは該当記事をご参照ください)。
このような数式で記述された最適化問題は、プログラムとして実装し、最適解を導出することで、業務上の意思決定に応用されます。
しかし、このような定式化やプログラムの実装には、数理的な知識に加えて、プログラミングスキルといった高度な専門性が求められます。そのため、現場で課題を抱える方々が自ら数理最適化モデルを構築・運用するには技術的なハードルが高く、専門家の支援が不可欠となるケースも少なくありません。
生成AIの台頭
近年、読者の皆さまもご存じのとおり、ChatGPT や Gemini に代表されるアプリケーションの登場により、生成AIは大きな注目を集めています。生成AIの活用によって、日々の生活や業務の在り方が大きく変わったと感じている方も多いのではないでしょうか。
NTTドコモビジネスにおいても、生成AIに関する取り組みが積極的に進められており、次のような公開情報からもその一端をご覧いただけます(生成AI(Generative AI)|NTTドコモビジネス 法人のお客さま)。また、Node-AIも、ユーザーによって自由度の高い可視化や前処理を支援するために、生成AIを活用したサポート機能が提供されています。詳しくは以下のリソースをご参照ください。
このような流れを受け、私たちは現在、数理最適化問題の定式化やプログラム実装のプロセスを、生成AIによって支援・自動化する研究に取り組んでいます。
具体的には、業務課題を自然言語で入力するだけで、生成AIが最適化問題としての構造を理解し、目的関数や制約条件を抽出・提案する仕組みの構築を目指しています。また、その数理モデルをもとに、ソルバーと連携可能なコードを自動生成することにも取り組んでおり、これにより、これまで専門家の手を要していたプロセスの大幅な効率化が期待されます。
このアプローチにより、数理最適化の専門知識を持たないユーザーでも、業務課題に対して数理最適化技術を活用しやすくなり、より多くの現場で高度な意思決定支援が実現できると考えています。
実現アプローチの検討
本章では、スーパーマーケットの発注量最適化をテーマに、生成AIを支援技術として取り入れた数理最適化の活用について検討していきます。
生成AI活用の全体像
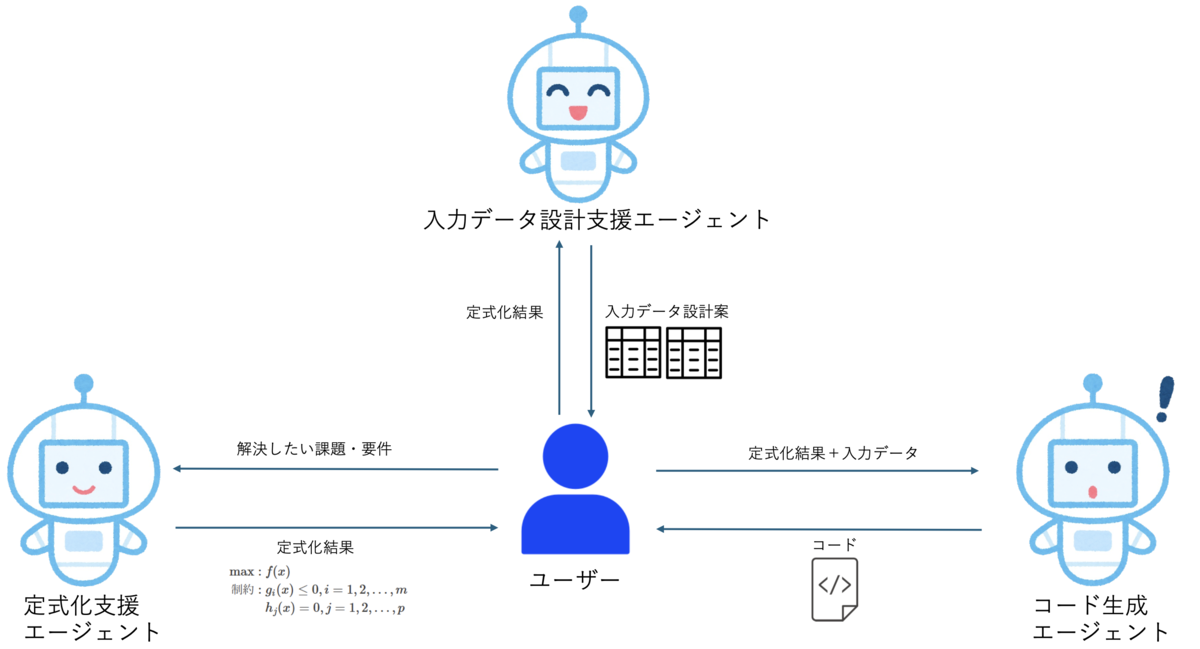
最初に、生成AI活用の全体像を示します。本アプローチでは、以下の3種類のAIエージェントを活用します。
- 定式化支援エージェント: ユーザーが抱えている課題や要件をプロンプトとして入力するだけで、AIが数理最適化モデルを自動で定式化します。
- 入力データ設計支援エージェント: 定式化された数理モデルに基づき、数理最適化実行に必要なデータ構造の設計案を具体的な例とともに提案します。
- コード生成エージェント: 定式化されたモデルと設計された入力データをもとに、数理最適化を実行するためのプログラムコードを自動生成します。
これら3種類のAIエージェントが連携してユーザーをサポートすることで、これまで専門知識が不可欠であった数理最適化技術の導入プロセスを大幅に簡素化し、現場への迅速な実装を可能にします。
次のフローは、上記のAIエージェントを補助的に活用し、業務課題を解決するための数理最適化モデルの定式化から実行コードの生成、さらに業務への実装に至るまでのプロセスを体系的に整理したものとなっています。
① 課題の適性診断(担当:定式化支援エージェント)
ユーザーが解決したい課題の概要を定式化エージェントに入力。その課題が数理最適化技術での解決に適しているかの判定。
- 解決可能と判定された場合: ステップ2への移行。
- 解決困難と判定された場合: 別のアプローチ(機械学習、シミュレーションなど)の検討。
② 数理モデルの定式化(担当:定式化支援エージェント)
ユーザーによる課題詳細(制約条件、目的関数など)のエージェントへ入力。これを数理最適化問題として定式化し、その内容をMarkdownファイルとして出力。
③ 入力データの設計(担当:入力データ設計支援エージェント)
ステップ2で作成された数理モデルのMarkdownファイルを、入力データ設計支援エージェントへインプット。モデルに必要なデータ項目の自動抽出および機械学習による予測の必要性の有無の判断、それらのデータ設計方法の具体例を伴う提示。
④ 入力データの準備(担当:ユーザー)
ステップ3の設計案に基づく、実際の業務データなど必要な入力データの準備。
- (分岐): ステップ3で機械学習による予測が必要と判断されたデータ項目については、Node-AIなどのツールを用いた予測モデルの構築と、それによる予測値の生成。
⑤ 実行コードの生成(担当:コード生成エージェント)
ステップ2の数理モデルのMarkdownファイルと、ステップ4の入力データをコード生成エージェントへインプット。特定の最適化ライブラリを使用した実行可能なPythonコードの生成。
⑥ 業務への実装と活用(担当:ユーザー <+コード生成エージェント>)
生成されたPythonコードの、ユーザーによる実際の業務プロセスやシステムへの組み込み。コードの微調整や運用方法の最適化など、コード生成エージェントのサポートを適宜受けながらの業務利活用の推進。
なお、各種AIエージェントの支援を活用し、上記プロセスを通じて業務課題への数理最適化技術の適用を容易にするアプリケーションを開発しています。
本稿では、その開発中の画面の一部とともにご紹介します。
在庫最適化の課題設定
次に、本検討で取り上げる課題設定を示します。なお、課題はシンプルに設定しています。
○ 目的
スーパーマーケットにおける日配品の在庫管理を対象に、適正在庫を維持しながら、廃棄ロスを最小限に抑えることを目指す。欠品はある程度許容しつつ、過剰在庫によるロスの削減を重視する。
○ 前提条件
- 対象カテゴリ:日配品
- 対象商品数:50SKU (Stock Keeping Unit: 在庫管理単位)
- 発注頻度:毎日
- リードタイム:1日
- オペレーション:
- 午前中に発注指示
- 閉店後、消費期限切れ商品を廃棄
- 翌朝、発注商品が納品
- 納品体制:地域の卸業者による一括納品
イメージ図(AI生成)

以降では、こちらの課題を例に、AIエージェントを活用した具体的なフローを説明します。
実現までのステップ
1. 定式化支援エージェントによる定式化支援
まず、数理最適化に不慣れなユーザーにとっては、前述した在庫管理の課題が数理最適化によって解決可能かどうかを判断するのは容易ではありません。そこで、生成AIを活用し、当該課題が数理最適化の適用対象となり得るかを診断するアプローチを試みます。
以下は、当該課題に数理最適化技術を適用できるかどうかを判断するために、定式化支援エージェントに与えるプロンプトの一例です。現在開発中のアプリケーションでは、ユーザーが【課題概要】の欄に自身の課題を簡潔に入力すると、これをもとにエージェントが応答を生成する仕組みになっています。
エージェントによる回答結果はこちらです。
定式化支援エージェントの解析結果として、「数理最適化によって解決可能である」との判断が得られました。これを受け、次のステップでは、具体的な数理最適化問題の定式化に進みます。
下記は、定式化支援エージェントに数理最適化問題の定式化を依頼する際のプロンプト例です。開発中のアプリケーションでは、ユーザーが【課題内容】欄に具体的な課題を入力すると、それを踏まえてエージェントが最適な定式化を自動生成します。
定式化支援エージェントからは、次のような回答が得られました。
定式化支援エージェントを用いることで、数理最適化問題の定式化がわずか1分足らずで完了しました。通常であれば、人手による定式化には相応の時間と労力を要しますが、エージェントは非常に短時間で処理を行い、大幅な時間短縮を実現しています。
作成された定式化には、プロンプトで与えた「目的」や「制約」、「補足情報」が的確に反映されており、日本語による説明を通じて、その妥当性が確認できます。
特に注目すべきは、欠品量・廃棄量・在庫の遷移といった要素について、プロンプト内で明示的に指示していないにもかかわらず、適切に定式化へ組み込まれていた点です。
さらに、消費期限順に商品が販売・消費されるという数式で表現するには難易度の高い制約についても、エージェントは短時間で的確に反映しており、その高い汎用性と柔軟性がうかがえます。
本エージェントにより定式化された数理最適化モデルが妥当と判断された場合、生成AIを用いてMarkdown形式で内容の整理・保存を行います。これを次のステップの入力データ設計支援エージェントに引き渡していきます。
2. 入力データ設計支援エージェントによるデータ設計支援
前節では、定式化支援エージェントのサポートを受けながら、数理最適化問題の定式化を完了しました。次に、最適化を実行するために必要な入力データの設計を行います。
不慣れなユーザーにとっては、「どのようなデータを、どのような構成で用意すればよいのか」が分かりにくい場合があります。そこで本アプリケーションでは、入力データ設計支援エージェントを活用して、入力データの設計案を自動的に提示する仕組みを取り入れています。
数理最適化モデルが記述されたMarkdownファイルをアップロードした上で、入力データ設計支援エージェントに次のようなプロンプトを与えます。なお、開発中のアプリケーションにおいては、自動でこのプロンプトが与えられます。
エージェントによる回答結果はこちらです。
まず、Step 1ではデータ項目の整理を行っています。具体的には、「データ項目」「説明」「数式表現」「単位例」「カテゴリ」「機械学習(回帰)を要する可能性」の6項目が一覧化されています。
このステップで特に注目すべきなのは、「機械学習(回帰)を要する可能性」の判定結果です。機械学習に詳しくないユーザーにとって、あるデータを準備するのに機械学習技術が必要かどうかを判断するのは容易ではありません。この判定結果は、その判断をサポートする重要な情報となります。
例えば、「需要量」については機械学習技術の活用が必要と判断されています。実際、将来の需要量を見積もるには予測が伴うため、機械学習手法を用いる必要があります。
Step 2では、CSVファイル形式による入力データの設計案が提示されており、各ファイルの名称や具体的なデータ例も示されています。今回の例では、以下の4つのCSVファイルに分割して設計することが提案されています。
-
products.csv(商品ごとの基本情報を示すデータ)※「欠品コスト(円/個)」および「廃棄コスト(円/個)」の値は、ユーザーの業務内容やポリシーに応じて個別に設定する必要があります。例えば、簡易的な想定として、欠品コストは粗利、廃棄コストは仕入れ価格を基準とすることが可能です。
-
demand.csv(各商品における将来の需要数(予測値)を示すデータ) initial_inventory.csv(各商品の初期在庫量を記録したデータ)scalar_constraints.csv(計画期間といった全体に適用される設定値)
この設計案を参考に、次節では実際のデータ準備を進めていきます。
3. Node-AIを活用したデータの準備
前節のエージェントによる出力結果を参考にしながら、必要な入力データを実際に準備していきます。なお、データの取得にあたっては、場合によっては既存の業務プロセスに対する見直しや調整が必要となる可能性もあります。
まず、「機械学習(回帰)を要する可能性」が「あり」と判定された「商品の需要量」に着目します。この項目は機械学習による予測が必要であるため、NTTドコモビジネスのプロダクトであるNode-AIを活用します。Node-AIのキャンバスは以下の画像の通りです。操作手順については、こちらの記事で紹介している内容と基本的には同じであるため、本稿では詳細な説明を省略します。
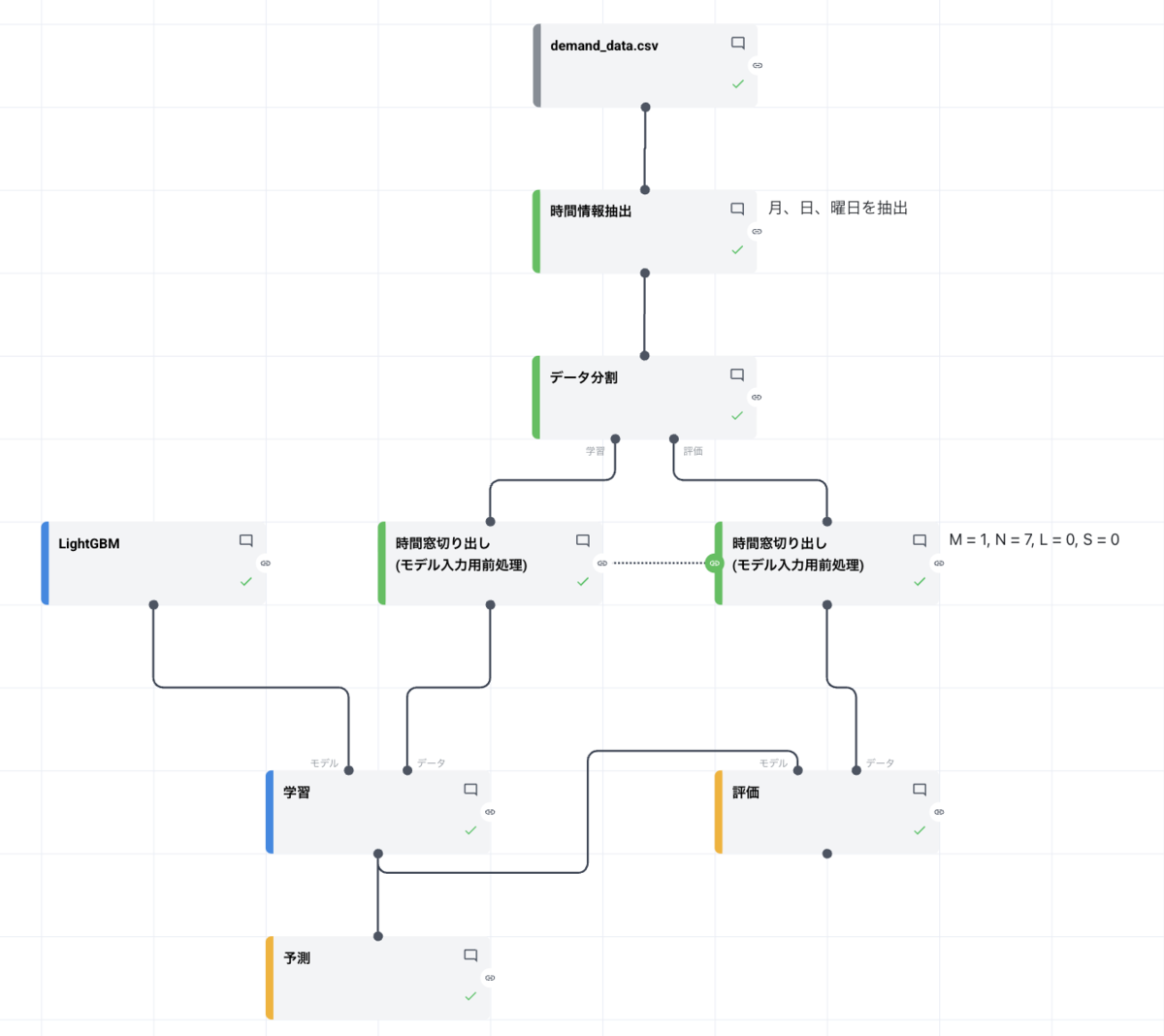
この予測結果に加え、Step 1で提示された「説明」やStep 2の入力データ設計案を踏まえて、実際の入力データの整備を進めます。今回は、以下のような形式でデータを準備しました。
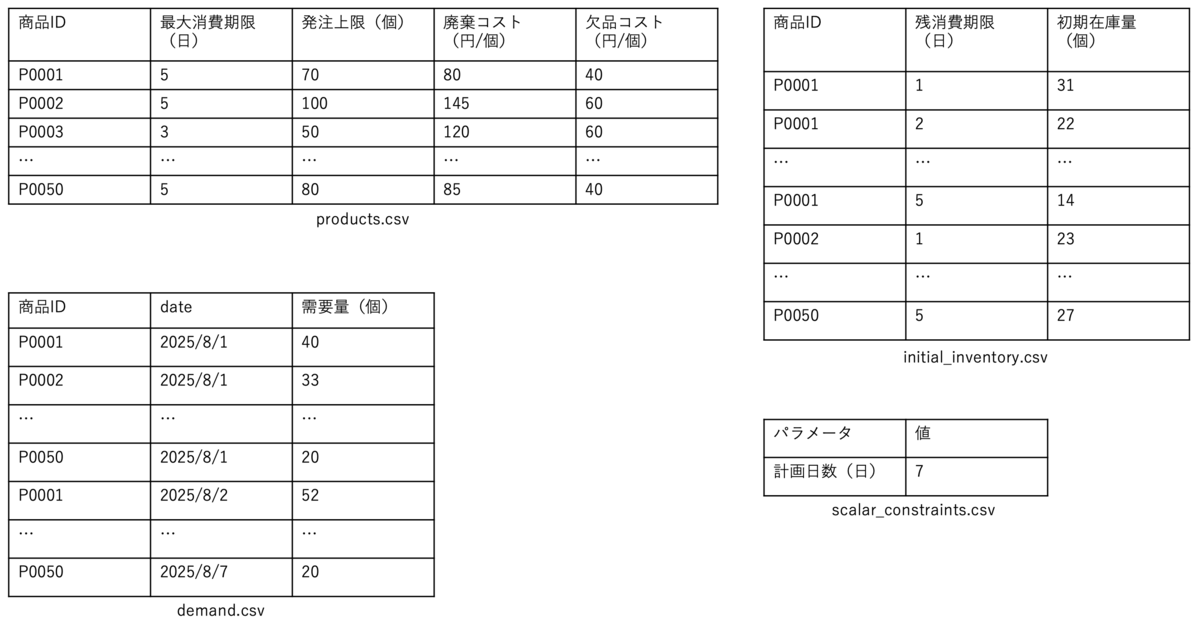
なお、Step 2で提示されている入力データ設計案はあくまで一例であり、その形式に厳密に従う必要はありません。ユーザーの業務環境や保有するデータの構造に応じて、列名やデータ型などを柔軟に調整して問題ありません。
例えば今回の例だと、initial_inventory.csv における列名「消費期限クラス」を「残消費期限(日)」に変更しており、demand.csvの日付形式も「yyyy-mm-dd」から「yyyy/mm/dd」へと変更しています。
こうして必要に応じた調整を行いながら、数理最適化の実行に必要なデータを整備しました。
4. コード生成エージェントによる実行コード生成
データの準備が完了したので、最後にコード生成エージェントを活用して数理最適化を実行するための Python コードを作成します。なお、コードの実行は以下の環境で検証しています。
version
Python: 3.13.1
PySCIPOpt: 5.2.1
SCIPソルバー: 9.2.0
numpy: 2.2.2
pandas: 2.2.3
準備した入力データのCSVファイルと、数理最適化モデルが記述されたMarkdownファイルをアップロードし、その上でコード生成エージェントに次のプロンプトを与えます。なお、開発中のアプリケーションではこちらのプロンプトに関してもあらかじめ設定されていて、自動で操作が行われます。
エージェントによって出力された結果は以下の通りです。
import pandas as pd from pyscipopt import Model, quicksum class Solver: def __init__(self, scalar_constraints_path: str, demand_path: str, inventory_path: str, product_path: str): """ Solverクラスの初期化 :param scalar_constraints_path: スカラーの制約定数が入ったCSVファイルのパス :param demand_path: 需要データCSVファイルのパス :param inventory_path: 初期在庫CSVファイルのパス :param product_path: 商品パラメータCSVファイルのパス """ self.scalar_constraints_path = scalar_constraints_path self.demand_path = demand_path self.inventory_path = inventory_path self.product_path = product_path self.model = Model("perishable_inventory") def load_data(self): """ CSVファイルから各種データを読み込み、 モデルで使うパラメータを準備する """ self.scalar_constraints_df = pd.read_csv(self.scalar_constraints_path, encoding="shift_jis") self.scalar_constraints_df.set_index("パラメータ", inplace=True) self.demand_df = pd.read_csv(self.demand_path, encoding="shift_jis") self.inventory_df = pd.read_csv(self.inventory_path, encoding="shift_jis") self.product_df = pd.read_csv(self.product_path, encoding="shift_jis") self.T = int(self.scalar_constraints_df.loc["計画期間(日)", "値"]) self.products = list(self.product_df["商品ID"].unique()) self.S = self.product_df.set_index("商品ID")["最大消費期限(日)"].to_dict() self.U = self.product_df.set_index("商品ID")["発注上限(個)"].to_dict() self.c_w = self.product_df.set_index("商品ID")["廃棄コスト(円/個)"].to_dict() self.c_s = self.product_df.set_index("商品ID")["欠品コスト(円/個)"].to_dict() unique_dates = sorted(self.demand_df["date"].unique()) self.date_to_t = {d: idx + 1 for idx, d in enumerate(unique_dates)} self.d = {} for _, row in self.demand_df.iterrows(): i = row["商品ID"] t = self.date_to_t[row["date"]] self.d[(i, t)] = int(row["需要量(個)"]) self.I0 = {} for _, row in self.inventory_df.iterrows(): i = row["商品ID"] s = int(row["残消費期限(日)"]) self.I0[(i, s)] = int(row["初期在庫量(個)"]) def build_model(self): """ 数理モデルの構築 変数定義、目的関数設定、制約条件設定を行う """ self.load_data() self.x = {} self.I = {} self.f = {} self.b = {} self.w = {} for i in self.products: Si = self.S[i] Ui = self.U[i] for t in range(1, self.T+1): self.x[(i, t)] = self.model.addVar( vtype="INTEGER", lb=0, ub=Ui, name=f"x_{i}_{t}" ) self.b[(i, t)] = self.model.addVar( vtype="INTEGER", lb=0, name=f"b_{i}_{t}" ) self.w[(i, t)] = self.model.addVar( vtype="INTEGER", lb=0, name=f"w_{i}_{t}" ) for s in range(1, Si+1): self.I[(i, t, s)] = self.model.addVar( vtype="INTEGER", lb=0, name=f"I_{i}_{t}_{s}" ) self.f[(i, t, s)] = self.model.addVar( vtype="INTEGER", lb=0, name=f"f_{i}_{t}_{s}" ) self.model.setObjective( quicksum( self.c_w[i] * self.w[(i, t)] + self.c_s[i] * self.b[(i, t)] for i in self.products for t in range(1, self.T+1) ), "minimize" ) for i in self.products: Si = self.S[i] for s in range(1, Si+1): init_val = self.I0.get((i, s), 0) self.model.addCons( self.I[(i, 1, s)] == init_val, name=f"initInv_{i}_{s}" ) for i in self.products: Si = self.S[i] for t in range(2, self.T+1): for s in range(1, Si+1): if s == Si: self.model.addCons( self.I[(i, t, s)] == self.x[(i, t-1)], name=f"invTrans_new_{i}_{t}_{s}" ) else: self.model.addCons( self.I[(i, t, s)] == self.I[(i, t-1, s+1)] - self.f[(i, t-1, s+1)], name=f"invTrans_{i}_{t}_{s}" ) for i in self.products: for t in range(1, self.T+1): demand = self.d.get((i, t), 0) Si = self.S[i] self.model.addCons( quicksum(self.f[(i, t, s)] for s in range(1, Si+1)) + self.b[(i, t)] == demand, name=f"demandFulfill_{i}_{t}" ) for i in self.products: for t in range(1, self.T+1): Si = self.S[i] for s in range(1, Si+1): self.model.addCons( self.f[(i, t, s)] "sellCap_{i}_{t}_{s}" ) for i in self.products: for t in range(1, self.T+1): demand = self.d.get((i, t), 0) Si = self.S[i] for s in range(1, Si+1): if s > 1: self.model.addCons( self.f[(i, t, s)] for k in range(1, s)), name=f"fifo_{i}_{t}_{s}" ) for i in self.products: for t in range(1, self.T+1): self.model.addCons( self.w[(i, t)] == self.I[(i, t, 1)] - self.f[(i, t, 1)], name=f"wasteDef_{i}_{t}" ) def solve(self): """ モデルを解く """ self.model.setParam('display/verblevel', 0) self.model.optimize() def check_model_status(self): """ 解の状態を確認し、最適解が見つかったかどうかを返す """ status = self.model.getStatus() if status == "optimal": print("✅ 最適解が見つかりました。") return True else: print(f"エラー:{status}") return False def get_solution(self): """ 最適解がある場合、各変数の値を辞書で取得する """ if not self.check_model_status(): return None best_sol = self.model.getBestSol() if best_sol is None: print("❌ 実行可能解は取得できませんでした。") return None result = {} for var in self.model.getVars(): val = self.model.getSolVal(best_sol, var) result[var.name] = val return result
コード生成エージェントを活用することで、このように長大なコードであっても、わずか1分足らずでミスなく作成できました。人手によるコーディングでは多くの手間や時間がかかりますが、エージェントによりそれらを大幅に削減し効率的な開発を可能にしています。
生成されたコードは、先ほど用意した4つのデータを読み込み、それをもとに最適な発注量や在庫の動きを計算する仕組みです。消費期限や在庫の状況、日ごとの需要などを考慮しながら、「どの商品を、いつ・どれだけ発注し、どのくらい販売し、欠品や余剰がどの程度発生するか」を自動的に判断します。
このようにして、在庫の無駄や欠品をできるだけ抑えた、バランスの取れた計画が立てられるようになります。
この Solver クラスを利用して、実務で使うために各商品の当日発注量をCSVファイルとして出力するコードを、エージェントに作成してもらいます。
エージェントに渡すプロンプトは以下の内容です。
エージェントによって作成されたコードはこちらです。
import argparse import pandas as pd from optimizer import Solver def export_first_day_orders( scalar_constraints_path: str, demand_path: str, inventory_path: str, product_path: str, output_csv_path: str ): """ Solver を使って最適化を実行し、 初日の各商品の発注量を CSV 出力する。 :param scalar_constraints_path: scalar_constraints.csv のパス :param demand_path: demand.csv のパス :param inventory_path: inventory.csv のパス :param product_path: product.csv のパス :param output_csv_path: 出力 CSV ファイルのパス """ solver = Solver( scalar_constraints_path=scalar_constraints_path, demand_path=demand_path, inventory_path=inventory_path, product_path=product_path ) solver.build_model() solver.solve() sol = solver.get_solution() if sol is None: print("最適解が取得できなかったため、CSV を出力しません。") return records = [] for product_id in solver.products: var_name = f"x_{product_id}_1" qty = sol.get(var_name, 0) records.append({ "商品名": product_id, "発注量": int(qty) }) df_out = pd.DataFrame(records, columns=["商品名", "発注量"]) df_out.to_csv(output_csv_path, index=False, encoding="shift_jis") print(f"初日の発注量を '{output_csv_path}' に出力しました。") if __name__ == "__main__": parser = argparse.ArgumentParser( description="初日の各商品の発注量を最適化し、CSV 出力します。" ) parser.add_argument( "--scalar_constraints", required=True, help="scalar_constraints.csv のパス(Shift_JIS)" ) parser.add_argument( "--demand", required=True, help="需要データ CSV のパス(Shift_JIS)" ) parser.add_argument( "--inventory", required=True, help="初期在庫データ CSV のパス(Shift_JIS)" ) parser.add_argument( "--product", required=True, help="商品パラメータ CSV のパス(Shift_JIS)" ) parser.add_argument( "--output", required=True, help="出力先 CSV ファイルのパス(Shift_JIS)" ) args = parser.parse_args() export_first_day_orders( scalar_constraints_path=args.scalar_constraints, demand_path=args.demand, inventory_path=args.inventory, product_path=args.product, output_csv_path=args.output )
エージェントを活用することで、こちらのコードも短時間でミスなく作成できました。
5. 作成されたコードの実行と結果
例えば、必要なデータファイルと出力ファイルのパスを指定し、次のようなコマンドを実行することで、
python export_first_day_orders.py \ --scalar_constraints scalar_constraints.csv \ --demand demand.csv \ --inventory initial_inventory.csv \ --product products.csv \ --output initial_orders.csv
以下のような各商品の当日発注量をまとめたCSVファイルが自動的に出力されます。こちらの情報をもとに各商品の発注作業を行います。
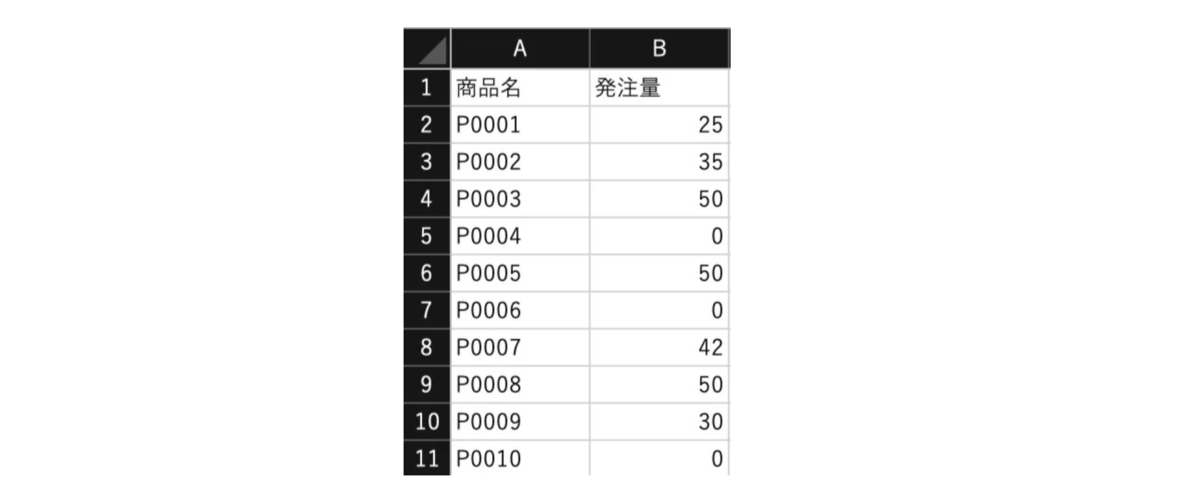
このように、生成されたコードを活用することで、業務で実際に必要となるファイルの作成までを一貫して自動化できます。現場でもすぐに運用に取り入れやすいため、これまで発注作業にかかっていた時間の大幅な短縮や、ヒューマンエラーの削減が期待されます。
まとめ
本記事では、生成AIを活用した数理最適化技術の自動化に関する検討をご紹介しました。特に、スーパーマーケットにおける在庫管理を一例として取り上げ、エージェント3種のサポートのもとで課題設定から実装に至るまでのプロセスを示しました。
本記事で一部をご紹介したアプリケーションは現在も開発中であり、引き続き改良を重ねてまいります。
今後は、生成AIの回答精度向上やUI/UXの改善に取り組むとともに、実社会での活用に向けた検証を進め、研究開発を一層推進していく予定です。
おわりに
本記事が少しでも皆さまのお役に立てたのであれば、嬉しく思います。
Node-AIを活用した機械学習技術のビジネス活用にご関心のある方は、ぜひこちらのフォームよりお気軽にお問い合わせください。
また、本記事の内容に関するご質問や、数理最適化技術をはじめとした数理解析技術のPoCにご関心のある方は、メールにてご連絡をお待ちしております。(メール:adam-ic[at]ntt.com)

